Self-Driving Car Behavior Modelling

Center for Multidisciplinary Research in Traffic

Note: This article is not yet complete 😭

This is work that I have done with Dr. Jia Li at Texas Tech University from January 2019 to May 2020. Dr. Li had to leave TTU and the US temporarily during the pandemic and we lost touch so we never got the chance to publish on this work. Nevertheless, find the article below as written during May of 2020.

Abstract:

We investigate spontaneous platoon formation in heterogeneous traffic flow consisting of human-driven (HVs) and autonomous vehicles (AVs) in different behavior scenarios through simulation experiments. Our study reveals that platoons may form spontaneously, and platooning properties are associated with the behaviors of AVs. We conduct the simulation experiments through a parsimonious Cellular Automata model (we develop a software for this purpose), which captures the different characters of AVs and HVs as well as their interactions. AVs are endowed with neighbor awareness and opportunistic behaviors. We observe that, intriguingly, even with this relatively simple model, AVs form into platoons without centralized control. Such phenomena may relate to the intrinsic incentives that AVs perceive and their ability to tell neighbor vehicle types. Our findings indicate the potential of regulating future heterogeneous traffic flow through decentralized agent behavior design.

Introduction

Driver-less cars (i.e., autonomous vehicles, henceforth called AVs) have already appeared on the road and shared right of way with human-driven vehicles (henceforth called HVs). An appealing feature of AVs is their capability to form platoons, which is anticipated to boost efficiency of traffic flow substantially. A number of recent research have delved into modeling and operations of the mixed flow of AVs and HVs, most of them attempted to capture or optimize the platooning feature of AVs.

Much attention in literature (see e.g. ) has focused on problems along the longitudinal dimension and adopt a microscopic approach, which embraces simulation of car-following behaviors, platoon control, and stability analysis. While the understanding of microscopic longitudinal behaviors of mixed AV-HV flow has become relatively mature, the collective behaviors to be anticipated in a multi-lane setting remain elusive, where the interplay of AVs and HVs can be substantially more complicated, due to the possibility of lane choice and lane changing. The lateral behaviors are coupled with longitudinal dynamics, and the two together determine dynamics of mixed AV-HV flow. Discussions along this line are still primitive, mostly focused on the estimation of mixed flow capacity (see e.g. ) and aggregate flow-density relation (see e.g. ). These works all assume the mixed flow is in perfect steady state does not explicitly consider lateral interactions in general multilane setting. Concerning the impacts of lanes on traffic flow, several empirical studies have been conducted towards understanding the impacts of HOV lanes on traffic in general purpose (GP) lanes, which revealed the existence of a smoothing effect caused by restriction of lane-changing. Past research also examines lane-to-lane traffic interactions on multilane highways, which include lane flow distribution , as well as impacts of microscopic lane-changes . On the theoretical side, it is only in limited cases that the connection between lane policy and traffic flow characteristics has been investigated, and in almost all studies, the policy considered is static. and both considered traffic consisting of regular and priority vehicles, and a number of special lanes are accessible only to the priority vehicles. Both regular vehicles and priority vehicles are endowed with the identical fundamental diagram. Nonetheless, these studies are focused on human-driven traffic flow and do not consider any AV-specific behaviors. discussed capacity of mixed flow of AVs and HVs on multi-lane freeway under different combination of static lane access policies, assuming traffic flow is steady. derived capacity of mixed AV-HV flow in a similar context, assuming the spatial distribution of mixed flow follows a Markov process. An interesting lateral policy considered in literature is intermittent bus lane (IBL), which offers priority to buses, but also allows other regular vehicles to use the lane when space is available. and conducted queuing analysis using the LWR model and derived corresponding roadway capacity as well as conditions when IBL will benefit the entire system.

The key challenge to model mixed flow dynamics of AVs and HVs lies in capturing agents’ longitudinal and lateral behaviors simultaneously, which should account for not only agents’ dynamical characters (e.g. their longitudinal speed and acceleration as functions of headway), but also agents’ decision-making, as well as how the decisions of individual agents aggregate. Such interactions in mixed flow of AVs and HVs is conceivably more complicated than mixed human-driving traffic due to the rich possibilities of AV behaviors. For instance, with the advanced sensing and communication capabilities, AVs may behave more opportunistically than HVs in seeking peers in its neighborhood, because this potentially allow them to form platoons with peers and benefit from more smooth driving and better traveling speed.

In this paper, we are interested in understanding the collective dynamics of AV-HV flow, as a result of the interactions between heterogeneous agents. In particular, we seek to answer the following research questions: when AVs are self-interested and individually controlled by themselves (as opposed to coordinated by system operator), will they be able to self-organize into platoons? And if so, what are the conditions for the self-organization to initiate and sustain? This research is partly inspired from the self-organized phenomena widely existing in biological systems, such as army ants , where orders emerge when agents interact with each other locally. In traffic flow literature, similar self-organized phenomena were also reported .

To answer the above questions, we propose a Cellular Automaton (CA) model to encapsulate the essential behavioral factors of AVs and HVs, and conduct simulation experiments to characterize the impact of these behavior factors on the formation of clusters in mixed traffic flow. The simulation experiments were conducted on a circular road with three lanes. We consider two alternatives of AV behaviors. In the first scenario, AVs behave like HVs, except the difference in free flow speed and braking probability. In the second scenario, AVs are assumed to be fully aware of vehicle types in neighborhood and opportunistic in gap seeking.

The major finding of this research is the self-organized formation of AV clusters and lanes without any centralized control. This finding may suggest clustering as an intrinsic property of mixed flow, when AVs and HVs interact, and AVs are endowed with opportunistic behaviors. The existence of self-organization, if turns out to exist in real mixed flow of AVs and HVs, may suggest the possibility of regulating their interactions through a decentralized approach.

The remaining part of the paper is organized as follows. We first introduce how we capture the different car-following and gap seeking behaviors of AVs and HVs through a Cellular Automata (CA) model. Then we describe the setup of simulation experiments along with results and discussion. In this section, we focus on the flux of mixed flow as well as the formation process of AV clusters in different behavioral scenarios. Self-organized behaviors are observed in both models of AV behavior. We summarize the findings and remark on future works in the last section.

A Herding Model

Here we present a simple stochastic model to depict the essential idea behind our behavior design. We consider two classes of agents, respectively autonomous and human agents (denoted as $A$ and $H$ respectively). The agents are placed over grids a $M \times N$ grid, and each agent occupies one node.

We consider the following process. In each time step, two cells are randomly picked, and this 


We are interested in the equilibrium states of this system when $t \rightarrow \infty$.

Behavior Design and Implementation

Cellular Automata (CA) is a simple yet effective framework to model agent interactions over cells, which have found wide and successful applications modeling traffic flow. In CA, each agent occupies a cell, and its behavior is determined by its own state and the state of other agents in its neighborhood. Simple functions can be applied to these cell objects to change its state and as a result it can change the states of neighboring cells . Nagel and Schreckenberg (1992) were amongst the first to use this computational technique to model traffic flow .

Rules for CA models for traffic flow: (a) rules for single-lane highway (b) rules for multi-lane highway

CA is a discrete computational model in traffic flow literature that comprises a system of vehicles which evolve over linear time in accordance to rules (see e.g. ) summarized in Fig. 1; where, $v_j$ represents the speed of the car $j$, $v_{max}$ is the speed limit of the road, $d_j$ is the number of empty cells in front of car $j$, $x_j$ is the cell that car $j$ occupies, $v_{l’}$ is the number of empty cells in front of car $j$ if it were on lane, $l’$, and $d_{back}$ is the number of empty cells behind in the car in lane $l’$. Each update of the system, requires all the vehicles to follow these rules simultaneously, with each vehicle first deciding whether to change lane before deciding how much to move forward; this order of decision making is fundamental to the CA model.

In this paper, we adapt the Nagel-Schreckenberg Cellular Automaton model to introduce a model of mixed traffic flow of HVs and AVs that captures three potential behaviors of AVs - opportunistic, neighbor awareness and baseline behavior. We distinguish between the two class of vehicles in our simulation by assigning different behavioural parameters - braking probability, lane changing probability, maximum speed - and methods - traversal velocity functions - to each vehicle type and model.

Nomenclature

To avoid confusion with the various symbols used, we provide Table summarizing the conventions applied in this paper.

Symbol Description
$p_l(X)$ Probability of lane change for vehicle type $X$
$p_s(X)$ Probability of random slowdown for vehicle type $X$
$v^{av}(t)$ Velocity of AV at time-step $t$
$v^{av}_{max}$ Maximum speed an AV can attain
$v_{sl}$ Speed limit of the road
$s_{lv}$ Distance to the leading vehicle
$v^{hv}(t)$ Velocity of HV at time-step $t$
$v^{hv}_{max}$ Maximum speed an HV can attain
$v_{aa}$ Maximum speed of AV trailing another AV
$v_{ah}$ Maximum speed of AV trailing an HV
$v_h$ Maximum speed of HV
$v^L$ Velocity functions based on leading vehicle type
$v^L_{max}$ Maximum speed based on leading vehicle type
$\delta(p_s)$ Delta function (0 or 1) based on braking probability
$\delta(p_s(AV))$ Delta function for AV braking probability
$P(AV)$ Proportion of AVs in traffic
$P(AV-AV)$ Probability of an AV trailing another AV

Opportunistic Behavior

Autonomous Vehicles rely on algorithmic control for decision-making . This allows AVs to achieve idealized traffic flow parameters beyond HVs, whose speed can fluctuate due to human behavior and external conditions. AVs, unaffected by such variability, make acceleration and deceleration decisions based solely on safety and opportunity. When changing lanes, AVs do so only when it is both safe and beneficial, unlike HVs, whose behavior depends on driver aggressiveness. We capture this opportunistic AV behavior with the following conditions:

\begin{equation} p_{l}(HV) < p_{l}(AV) \end{equation} \begin{equation} p_{s}(HV) > p_{s}(AV) \end{equation}

In our model, $p_{l}(HV)$ and $p_{s}(HV)$ create realistic, stochastic HV behavior, while $p_{l}(AV) = 1$ and $p_{s}(AV) = 0$ for AVs reflect pure opportunistic behavior. The traversal velocity update equation capturing distinct AV behavior is:

\begin{equation} v^{av}(t+1) = \min(v^{av}(t) + 1, s_{lv}, v_{max}^{av}, v_{sl}) \end{equation}

Here, $v^{av}(t) + 1$ represents acceleration.

Neighbor Awareness

AVs communicate through V2X technology , allowing them to be aware of their surroundings, including nearby AV locations . Neighbor-aware AVs can maintain a shorter headway and higher speed when trailing another AV, behavior not applicable when following an HV. HVs remain unaffected by the class of the vehicle they follow. To model this, we redefine $v_{max}$ based on the leading vehicle type:

\begin{equation} v_{max}= \left{ \begin{array}{ll} v_{aa} & \text{if } AV-AV
v_{ah} & \text{if } AV-HV
v_{h} & \text{if } HV
\end{array} \right. \label{eq:v} \end{equation}

In this model, the following condition holds:

\begin{equation} \label{eq:cond} v_{aa} > v_{ah} \geq v_{h} \end{equation}

From Equations \ref{eq:v} and \ref{eq:cond}, an AV trailing another AV attains the highest possible speed, $v_{aa}$, while an HV’s speed is capped at $v_{h}$, independent of the leading vehicle’s class. Velocity functions $v^L$ depend on the leading vehicle type, as shown in Fig . The traversal velocity update function for this model is:

\begin{equation} v^{av}(t+1) = \min(v^{av}(t)+1, s_{lv}, v_{max}^{L}, v_{sl}) - \delta(p_s(AV)) \end{equation}

Here, $v^{av}(t) + 1$ represents acceleration, and $\delta(p_s(AV))$ is a delta function based on AV braking probability:

\begin{equation} \label{deltas} & \delta(p_s(AV)) =
\left{ \begin{array}{ll} 1 & \text{if } p_s(AV) < X \text{ for } X \sim U(0,1)
0 & \text{otherwise}
\end{array} \right. \end{equation}

Baseline Behavior

In this model, AVs behave exactly like HVs, with identical behavior between the two. Traditional CA rules from Fig govern this behavior, with additional constraints ensuring behavioral uniformity:

\begin{equation} \label{eq:b1} p_{l}(HV) = p_{l}(AV) \end{equation} \begin{equation} \label{eq:b2} p_{s}(HV) = p_{s}(AV) \end{equation}

Both vehicle classes have the same braking and lane-changing probabilities (Eqns. \ref{eq:b1} and \ref{eq:b2}) and follow the same traversal velocity update equation:

\begin{equation} \label{eq:bv} v(t+1) = \min(v(t) + 1, s_{lv}, v_{max}, v_{sl}) - \delta(p_s) \end{equation}

Model Implementation

Our simulation and analysis program was written in Python3, with graphics created using the Pygame 1.9.6 module. The model was implemented using Object-Oriented Programming (OOP) principles, with the main objects being Road and Car. NaSch CA algorithms were implemented by passing functions to these data structures and controlling program flow. The code repository for this program is available at .

Simulation Experiments and Findings

After observing several simulation cases, we discovered that AVs in certain models and scenarios displayed strong self-organization phenomena. Starting from random initial states, AVs evolved into configurations where they moved close to one another for extended periods. The two most prominent types of self-organized events observed were: AVs moving closely together in different lanes and AVs moving closely together in the same lane. For these simulations, we define a cluster as follows:

\[\textit{A cluster is a group of 4 or more AVs, each at most 3 cells apart.}\]

This broad definition allows us to incorporate both self-organized platooning and lane-formation events under a single collective phenomenon. The prominence of one form of clustering over the other depends on factors such as the radius of the circular road, the proportion of AVs, HV distribution, and overall traffic density. For instance, longer circular roads, higher AV proportions, localized HV distributions, and lower traffic densities increase the likelihood of lane-formation clusters compared to platooning clusters.

The chosen cluster definition (4 AVs within 3 cells) is arbitrary, suited to a simulated road of 100 cells. This captures both the proximity and visual significance of clustering. Prior works (e.g., ) have explored clustering in non-autonomous flows (e.g., trucks and buses). Here, we examine similar phenomena in mixed HV-AV traffic flow, where effective clustering of AVs implies optimized traffic flow. Thus, we focus on AV behaviors conducive to strong clustering.

Simulation snapshot: cluster of 6 AVs (red)
Simulation snapshot: self-organized lane of 7 AVs (red)

We hypothesize that clusters naturally form due to the opportunistic nature of AVs, modeled through gap-seeking and braking behaviors (Section ). In the neighbor-aware model, AVs achieve smaller headways by trailing other AVs, leading to significant lane formation and platooning. This incentivizes AVs to change lanes aggressively to follow other AVs.

Experimental Setup

In this section, we discuss two experiments that examine the impact of three AV models—neighbor aware, opportunistic, and baseline—on traffic flow and emergent behavior patterns. We further explore combinations of these models: neighbor aware and opportunistic and baseline headway (allowing AVs to maintain smaller headways than HVs).

\begin{equation}\label{eqn:awareoppo} v^{av}(t+1) = \min(v^{av}(t)+1, s_{lv}, v_{max}^{L}, v_{sl}) \end{equation}

Parameter Neighbor Aware Opportunistic Neighbor Aware and Opportunistic Baseline Headway Baseline
$p_{l}(HV)$ 0.6 0.6 0.6 0.6 0.6
$p_{l}(AV)$ 0.6 1 1 0.6 0.6
$p_{s}(HV)$ 0.4 0.4 0.4 0.4 0.4
$p_{s}(AV)$ 0.4 0 0 0.4 0.4
$v_{aa}$ 5 4 5 4 3
$v_{ah}$ 4 4 4 4 3
$v_h$ 3 3 3 3 3

Each experiment was run on a circular road with three lanes (100 cells each), where vehicles start from an empty state and are distributed randomly with zero initial velocity. The vehicle type is allocated stochastically, with $P(AV) = 0.3$, representing the proportion of AVs.

Heterogeneous Dynamics Under Constant Traffic Densities

We simulated five AV models for 1200 time steps across three density regimes: 0.08 (low), 0.2 (critical), and 0.6 (high). Densities are normalized, with 1 representing jam density, and $P(AV)$ fixed at 0.3. Key parameters tracked included cluster numbers, sizes, survival times, and Clusterability (ratio of vehicles in clusters to total vehicles).

Results are summarized in Table and Figure . The cluster count, average survival time, and clusterability provide insights into AV clustering behavior across density regimes.

AV Model Low Density Cluster Count Low Density Survival Time Critical Density Cluster Count Critical Density Survival Time High Density Cluster Count High Density Survival Time
Opportunistic 1.04 17.15 2.05 61.95 4.85 1200
Neighbor Aware 1.07 7.01 1.64 31.45 4.81 1200
Baseline 0.0 0.0 1.52 17.75 4.68 1200
Baseline Headway 1.05 6.14 1.69 23.30 4.68 1200
Neighbor Aware & Opportunistic 1.04 20.75 1.89 97.67 5.04 1200

Survival times revealed that the baseline model clusters were transient, whereas opportunistic models led to more prominent, longer-lasting clusters.

AV-AV Pair Probability (Low Density)
AV Lane Changes Over Time (Critical Density)

The AV lane-changing behavior showed that opportunistic AV models had the highest rates across all regimes. This tendency was even more pronounced in the critical density regime, where lane-changing peaked across models.

Equilibrium Relation and Dynamics Under Varying Traffic Densities

This experiment varied system density linearly to jam density, running 100 time steps per density increment of 0.03 (normalized scale). Figure illustrates how flux, lane changes, and lane change rates evolved for each model.

Our findings suggest that opportunistic AV models performed best overall, with neighbor aware and opportunistic AVs yielding the highest throughput. Clustering provided significant benefits, especially in low to critical densities, as AVs optimized traffic flow by maintaining shorter headways and opening space for HVs.

Lane Change Dynamics: The number of lane changes highlighted behavioral distinctions. Opportunistic models led to high lane-changing rates, with neighbor aware and opportunistic AVs exhibiting “intelligent herding” behavior, wherein AVs minimized HV lane changes through self-organized clusters.

This herding effect had safety, design, and fuel implications, as AV clusters facilitated smoother traffic by restricting HV lane changes.

Analysis Plots for Increasing Density Regime
Total Number of Lane Changes (Opportunistic Model)

The study verifies that prominent clustering is unique to systems involving opportunistic intelligent agents capable of recognition. Our findings suggest it is possible to design AV behaviors that form self-organized clusters, enhancing traffic efficiency.

Further research will explore implications for road safety, traffic design, and fuel efficiency due to clustering and herding dynamics.

Conclusion

In this paper, we investigated the behavior of mixed traffic flow consisting of AVs and HVs through a series of simulation experiments. Our primary goal was to explore the relationship between the opportunistic behaviors of AVs and the formation of clusters and lanes without centralized control. To achieve this, we developed a new cellular automata model that captures potential behavioral differences between AVs and HVs, particularly focusing on the gap-seeking behaviors and neighbor awareness of AVs. We conducted simulation experiments across two scenarios: fixed densities and linearly increasing densities, allowing us to compare the clustering process and traffic performance of three AV models.

A key finding of this research is the self-organized formation of AV clusters and lanes without centralized control, even in the absence of dedicated AV lanes. This phenomenon, observed consistently across simulations, suggests that clustering may be an intrinsic property of mixed HV and AV flows. We hypothesize that this self-organization results from incentives that encourage AVs to seek and align with other AVs. Opportunistic behaviors amplify this effect, as seen in our experiments. If confirmed through further simulation or real-world experiments, this hypothesis suggests that regulating mixed HV-AV flow might be achievable through decentralized incentives rather than centralized coordination. Our results also indicate a positive impact of clustering on overall traffic flow.

The findings in this paper provide initial evidence of self-organization in mixed AV-HV traffic flows. However, we acknowledge that our model is not quantitatively realistic. Since large-scale AV deployments are not yet in place, data on AV behaviors is limited, and the opportunistic behaviors we modeled are merely one plausible scenario. Future research, as more data becomes available, should aim to model AV decision-making more realistically and further validate the findings presented here.

Acknowledgement

This research was partially supported by a Seed Grant from the Hurricane Resilience Institute (HuRRI).

Appendix

Traditional Cellular Automata Rules

Road - Car grid in Cellular Automata

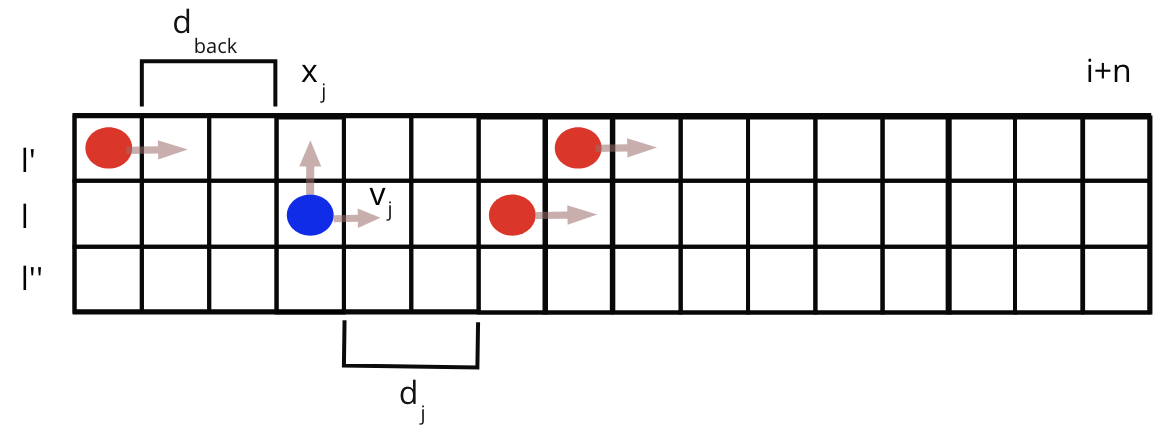
Figure 1: Road - Car grid in Cellular Automata

$P(\text{AV-AV})$ Algorithm

\label{pavav}

The following algorithm calculates $P(\text{AV-AV})$, which represents the probability of an AV trailing another AV. This value is calculated as the ratio of the running total of AV-AV pairs to the running total of all car pairs.

# P(AV-AV) Calculation Algorithm
def calculate_p_av_av():
    update = 0
    trailing_av = 0
    trailing_car = 1  # Assumes circular road and num(Car) > 1

    while simulation_is_running():
        timestep += 1
        if av_trailing_av():
            trailing_av += 1
            trailing_car += 1
        else:
            trailing_car += 1
        p_av_av = trailing_av / trailing_car  # Update at each timestep
    return p_av_av

NaSch CA Traffic Flow Analysis Software

The GitHub repository NaSch_CA_Traffic_Flow_Analysis_Software contains all simulation and analysis software developed for this research. It also includes the data files used in this paper. ```