Transmittance of Light through Air-Water Boundaries at Different Optical Depths
Freshman Year Math Project
Introduction
In our project, we analyze the path lengths of light waves as they traverse air-water boundaries. We model light scattered by clouds, impacting a still water surface, and reaching points beneath this surface at varying depths. Initially, we apply the Lambert-Beer equation to this scenario. We then introduce a more accurate model accounting for refraction at the air-water interface and track angle changes in incidence and refraction. The goal is to assess model accuracy and compute discrepancies with the Lambert-Beer model.
We have used Lambert Beer’s equation to first model this situation and then modeled the same situation using our equation. Our equation takes into account the refraction of light as it passes the air-water boundary, and makes use of the rates of change of incident and refractive angles. The objective of our paper is to test the accuracy of our model and compute the error factor between the two models (if any).
The Problem:
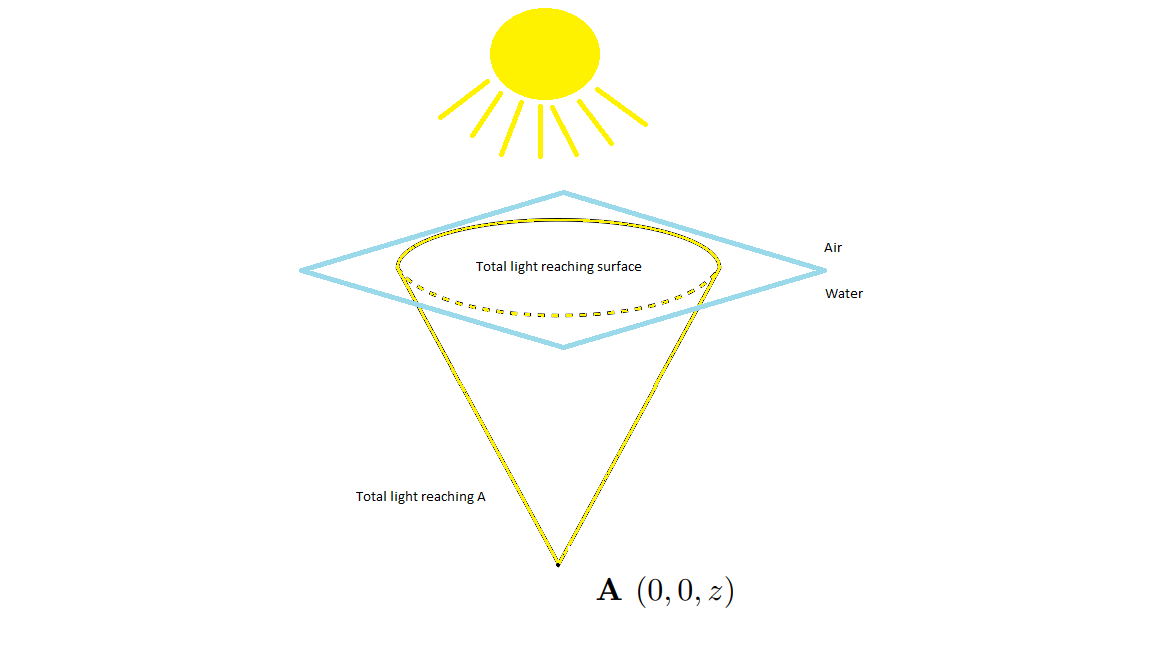
The problem is to calculate the total light reaching a certain point below the water surface on a cloudy day. The point of evaluation was taken to be an arbitrary point A with position: $(x,y,z)=(0,0,z)$.
Modeling assumptions used throughout both models were as follows:
- There was no wave motion on the surface of the water
- The sun was vertically above point A in the sky
- The temperature, density, and pressure of both air and water were assumed constant throughout
- The refractive index of water, $n_{w}$, was taken as 1.334 at all depths
- The optical density of water was assumed constant at all depths
- The light hitting the surface of the water was randomly scattered by clouds
Lambert-Beer Model:
According to Lambert Beer law, light reaching a certain point in an optically dense medium is modeled by:
\[p = p_{0} e^{a n (z - z_{0})}\]where $p$ is the number of photons per area, $n$ is the number of atoms per volume of the transmission medium, $a$ is the effective area of each atom, and $z$ is the depth of the point where the light reaches in the medium.
For our problem, this simplifies to:
\[p = e^{-z}\]Equation (1) calculates the total amount of light reaching point A.
Proposed Model:
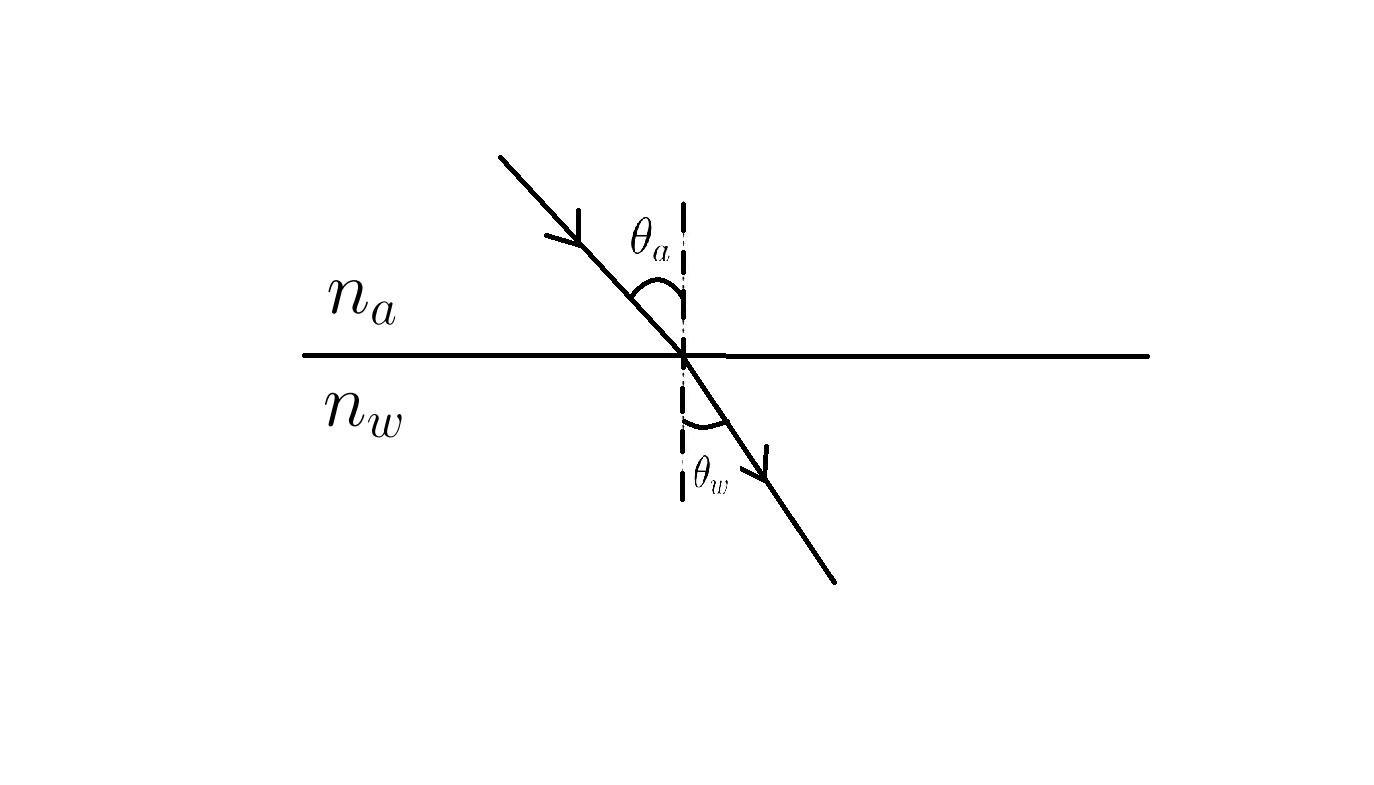
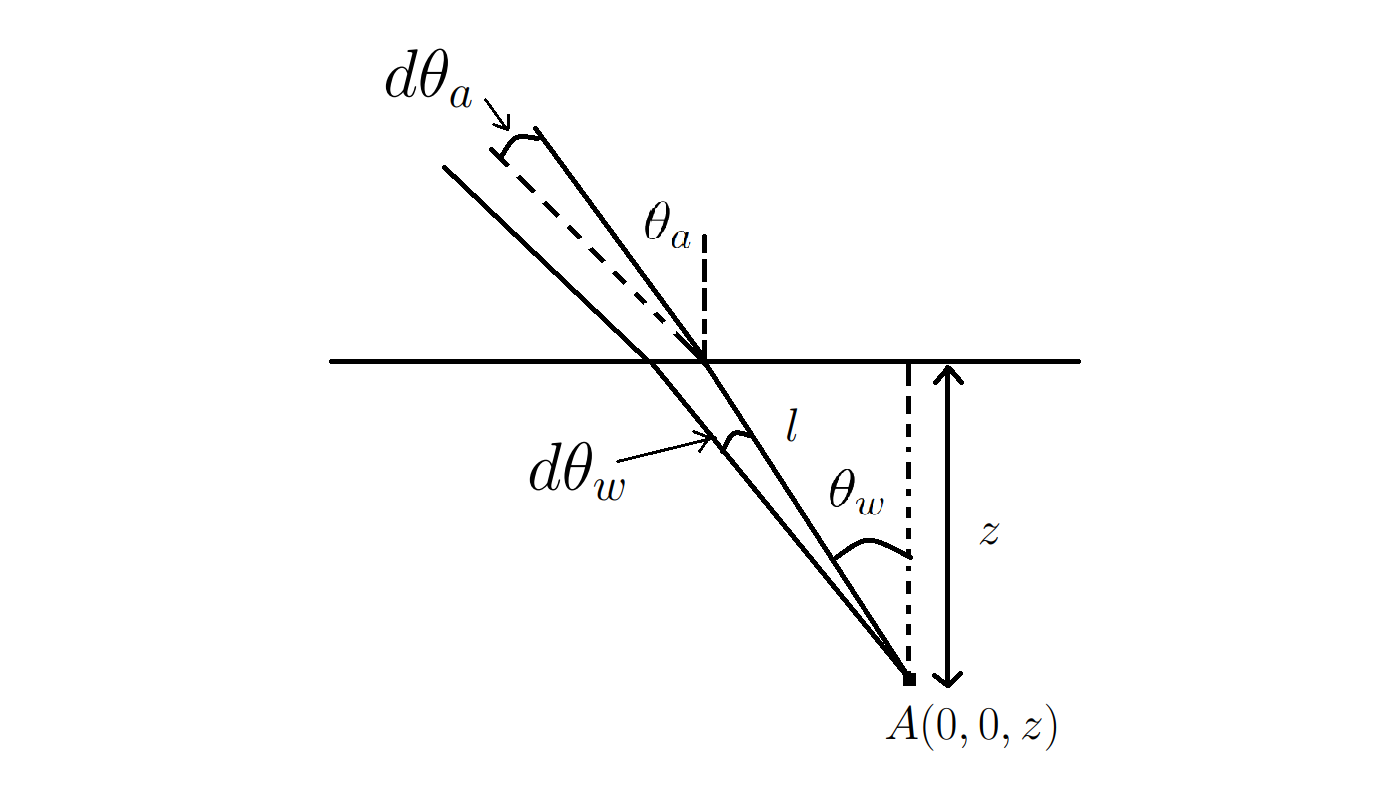
From Figure 3, we can write the path length, $l$, of the light ray as a function of $z$ and $\theta_{w}$:
\[l = \frac{z}{\cos{\theta_{w}}}\]Let $S_{a}$ be the light incident on the water surface per unit rad. Thus, the total light hitting water at any point is:
\[\int^{\pi/2}_{-\pi/2} S_{a} d\theta_{a} = \pi S_{a}\]Accounting for the refraction of incident light rays and integrating over the region where $\theta_{w}$ is between $(\theta_{max}, -\theta_{max})$, we get Equation (4), where $R(l)$ represents the total light reaching point A:
\[R(l) = \int^{\theta_{max}}_{-\theta_{max}} e^{kl} \frac{d\theta_{a}}{d\theta_{w}} d\theta_{w}\]Substituting $l$ from Equation (2) into Equation (3), we get:
\[R(z) = \int^{\theta_{max}}_{-\theta_{max}} e^{-\frac{k z}{\cos{\theta_{w}}}} \frac{d\theta_{a}}{d\theta_{w}} d\theta_{w}\]We use Snell’s law:
\[n_{a}\sin{\theta_{a}} = n_{w}\sin{\theta_{w}}\]Differentiating Snell’s law with respect to $\theta$ gives:
\[\frac{d\theta_{a}}{d\theta_{w}} = \frac{n_{w}}{n_{a}} \frac{\cos{\theta_{w}}}{\cos{\theta_{a}}}\]From Equation (6), we can write $\cos{\theta_{a}}$ as:
\[\cos{\theta_{a}} = \sqrt{1 - \left(\frac{n_{w}}{n_{a}}\right)^{2} \sin^{2}{\theta_{w}}}\]Thus,
\[\frac{d\theta_{a}}{d\theta_{w}} = \frac{n_{w}}{n_{a}} \frac{\cos{\theta_{w}}}{\sqrt{1 - \left(\frac{n_{w}}{n_{a}}\right)^2 \sin^2{\theta_{w}}}}\]At $\theta_{max}$, the angle of incidence $\theta_{a} = \frac{\pi}{2}$, giving $\sin{\theta_{a}} = 1$. With $n_{w} = 1.334$ and $n_{a} = 1$:
\[\theta_{max} = \sin^{-1}\left(\frac{n_{a}}{n_{w}}\right)\]Combining Equations (7) and (8) into Equation (5), we obtain Equation (9):
\[R(z) = \int^{\theta_{max}}_{-\theta_{max}} \frac{n_0 e^{-\frac{kz}{\cos{\theta_w}}} \cos{\theta_w}}{\sqrt{1 - (n_0 \sin{\theta_w})^2}} d\theta\]Let $kz = \xi$, representing optical depth. Then,
\[R(\xi, n_{0}) = \int^{\theta_{max}}_{-\theta_{max}} \frac{n_0 e^{-\frac{\xi}{\cos{\theta_w}}} \cos{\theta_w}}{\sqrt{1 - (n_0 \sin{\theta_w})^2}} d\theta\]Integrating over a circular area on the water surface using the polar Jacobian, we obtain:
\[R(\xi, n_{0}) = \int^{\theta_{max}}_{-\theta_{max}} \frac{n_0 \pi \sin{\theta_{w}} \cos{\theta_w}}{\sqrt{1 - (n_0 \sin{\theta_w})^2}} e^{-\frac{\xi}{\cos{\theta_w}}} d\theta\]Equation (11) calculates the total amount of light that reaches point A.
Analysis
We compare Equation (11) to the Lambert Beer Equation (Equation (1)).
We plotted the integrand from Equation (11) against varying $\theta_{max}$ values from $0$ to $2\pi$ at different optical depths.
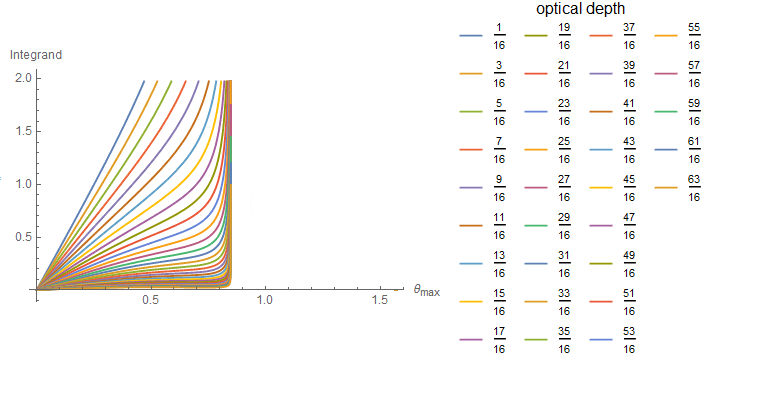
The figure shows the path lengths of light changing with different $\theta_{max}$ values and at different optical depths $z$. The graph is discontinuous around $\theta_{max} = \arcsin{\frac{1}{1.334}}$, as predicted. Light path lengths decrease exponentially at higher optical depths.
At optical depth $= 0$, $R(0, n_{0}) = 0.749625$. Using this result, we normalize Equation (11) into Equation (12):
\[\frac{R(\xi,n_{0})}{R(0,n_{0})} = \frac{\int^{\theta_{max}}_{-\theta_{max}} \frac{n_0 e^{-\frac{\xi}{\cos{\theta_w}}} \cos{\theta_w}}{\sqrt{1 - (n_0 \sin{\theta_w})^2}} d\theta}{0.749625}\]Plotting Equation (12) and the Lambert Beer Equation (Equation (1)) against optical depths $\xi \in (0.01, 10)$ in a log-log plot gives:
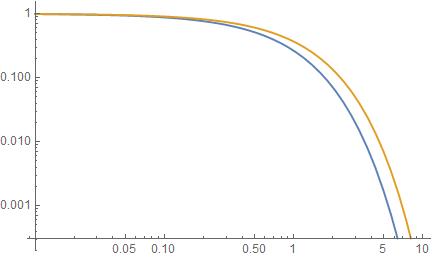
Both equations agree up to an optical depth of about $0.10$. At higher optical depths, significant differences arise due to refraction in Equation (11) but not in Equation (1), making our model more accurate than Lambert Beer’s.
To measure this error, we plot the ratio of Equation (11) and Equation (1) against optical depths $\xi \in (0.01, 10)$.
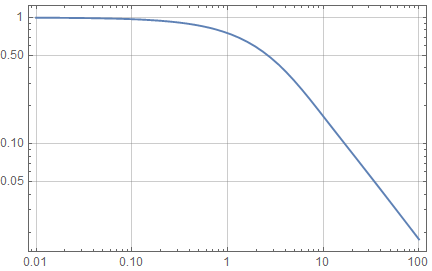
At optical depths greater than 0.1, the Lambert Beer equation deviates significantly from Equation (11), with discrepancies around $\xi = 7$ reaching a factor of approximately 2. This error rate grows rapidly at higher optical depths.
Conclusion
Our analysis shows that Equation (10) is more accurate than Equation (1) at higher optical depths. Lambert-Beer’s Equation approximates our equation at lower depths. Including light refraction is crucial at higher depths, proving Equation (11)’s relevance for applications in marine ecology, chemistry, optics, and other fields involving systems with high optical depths.